Okay, so this piece is going to take some time to explain because it combines some uncommon experimental composition ideas. So to make things short for those who don’t want to read something long and dry, I will begin by putting this in quick-and-dirty terms:

1. This is music co-written by my computer. I coded a piece of music that writes itself.
2. This piece utilizes notes and harmonies unavailable in “normal” music.

Point 1 is particularly oversimplified. So if you’d like a more detailed, accurate representation of what this is, read on.

A few months ago, I released Key West, an algorithmic/microtonal* piece that was composed using the awesome software known as Pure Data. While I really enjoyed how that piece turned out, I wanted to go further with Pure Data and create something that had stronger rhythmic content. Within a few days of completing it, I began putting together a new composition.

I put quite a few hours into it over the next few weeks. The code ended up a lot more complicated than I expected. I liked how it all came together, but upon finishing it… I felt that I couldn’t put it out yet. This was because I actually didn’t understand some of the theory behind what I had done, and didn’t know how I was possibly going to explain it. I was told that to someone who wasn’t already deep into lunatic-fringe musician territory, the explanation I wrote up for Key West was mostly incomprehensible gobbledygook, so I wanted to be sure that I could thoroughly explain this new one before I put it out to the public. I had to do some research to figure out what exactly I had come up with.

 

* Don’t know what these terms mean? Don’t worry, explanations are coming below.

 

MICROTONALITY

 

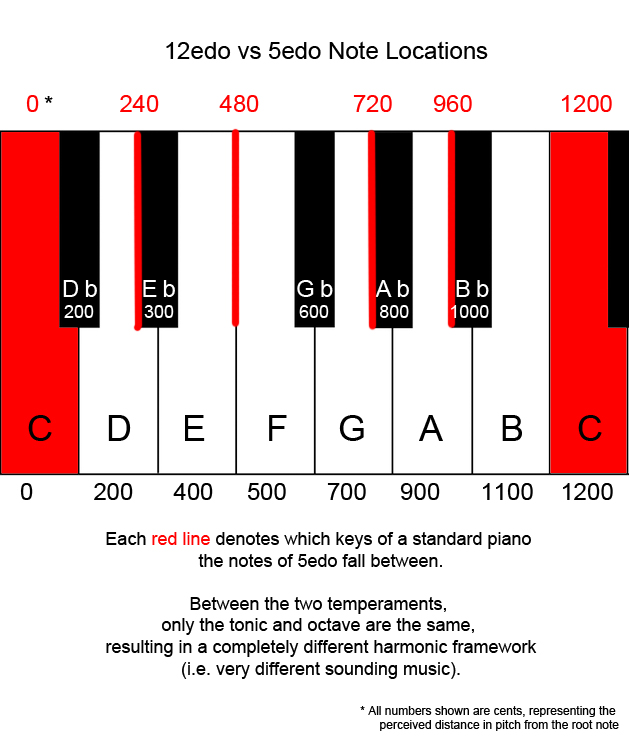
Like Key West, this piece also experiments with microtonality. Most music that we hear is written in 12edo (equal division of the octave), which splits the octave into 12 notes that the human ear interprets as even jumps in pitch. Key West utilizes a temperament known as 5edo, where the octave is split into 5 notes that the human ear interprets as even jumps in pitch, allowing the utilization of notes that are not found in most music.

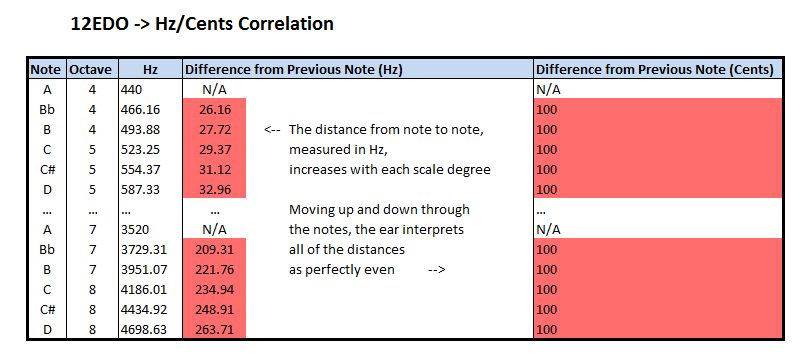
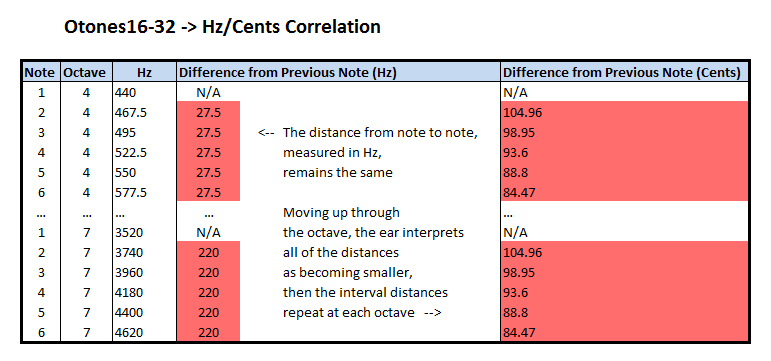
This song, however, abandons that approach and uses a different kind of system. The composition came to be as a result of my curiosity regarding different ways of splitting up the octave. After trying a bunch of different things, I happened to take the octave and split it up into 16 even divisions… but instead of splitting them up in equal cent intervals (tones that the human ear interprets as even jumps), like with an EDO, I split the octave evenly in hertz (i.e. vibrations per second). This is one of the things that I did that, at the time, I didn’t fully understand, and later got really confused by, so hopefully I can explain.

The human ear interprets frequencies logarithmically. Doubling any frequency will result in an octave harmony. We understand 200hz to be the same note as 100hz except one octave higher. This doubling continues with each iteration of the octave; 400hz, 800hz, 1600hz, et cetera are all perceived as the same note. This means that in a tuning system where every step of the scale is interpreted by the ear as being exactly even, the amount of Hz between each note increases.

So, as I said before, I derived the scale that I used for this piece in the opposite way. Instead of dividing evenly in cents, I divided the octave evenly into Hz. This means that as the scale increases, the ear interprets the intervals as getting closer together. I later learned that this is known as an otonal scale due to its relation to the overtone series (shout-outs to Dave Ryan and Tom Winspear for helping me figure out what the heck this approach is called).

This particular scale is known as otones16-32. From my research, otonal scales seem to be pretty uncommon. I don’t know why that is. They’re a very logical way to construct mathematically harmonious scales. To my ear, they can be utilized in a way which sounds very consonant, but they also allow for some exotic xenharmonic flavor.

From the 16 available notes in this scale, I chose a set of 7 of them that I thought sounded agreeable together. The ratios† of these notes are:

• 16/16 aka 1/1 aka unison
• 18/16 aka 9/8 aka major whole tone
• 19/16 (doesn’t reduce) aka overtone minor third
• 22/16 aka 11/8 aka undecimal tritone (11th harmonic)
• 24/16 aka 3/2 aka perfect fifth
• 25/16 (doesn’t reduce) aka augmented fifth
• 28/16 aka 7/4 aka septimal minor seventh
• 32/16 aka 2/1 aka octave

I found the sound of this scale inspiring (especially when I heard how strange it sounded to build chords with it), so I set out to put together a new algorithmic piece. Like I said earlier, I wanted to be more ambitious and give the thing more structure than my last effort.

 

† “Ratios? What does that mean in this context?” The ratio is what you multiply your base note by to create a particular harmony. For example, say your base note is 100hz. To create a perfect fifth (3/2), you multiply 100*(3/2), yielding 150hz. When 100hz and 150hz are played together, every time that the base note vibrates twice, the harmony vibrates exactly three times in perfect alignment.

 

 

ALGORITHMICALITY

 

An algorithmic composition, in its simplest form, is music that is made by creating and then following a set of rules. The term, however, is more commonly used for music where the artist designs some kind of framework (most often a computer program) that allows the piece to perform itself without intervention from the artist. In this case, I did just that: coded a framework of rules dictating which sounds are generated when by a combination of soundwave generators.

This composition also falls under a closely related musical form known as generative music. A composition is generative if it is unique each time that it is listened to. It needs to be continually reinventing itself in some way. This algorithmic composition is also a generative composition because the computer makes many determinations about the musical output each time that it is played. Every time the program runs and the song is heard, the chord progressions are different, as are the rhythms and notes that the instruments play. Many aspects of the composition are the same each time, but many others are determined by the computer and are unique to every listen.

 

Here are the rules I chose that are the same on every playthrough:

• The scale utilized
  • 7 notes of otones16-32
  • 1/1, 9/8, 19/16, 5/4, 11/8, 3/2, 25/16, 7/4, 2/1 (as explained above)
  • A base frequency of 200 (roughly halfway between G and Ab in A-440)
• The overall rhythm and tempo
  • 4/4
  • Backbeat on beat 3
  • 137bpm
• The intervals that the chord instrument plays
  • Root note, 3 notes up the scale, 5 notes up the scale
• The instruments and their beginning timbres
  • Drums
    • Kick
    • Snare
    • Hi-hats on both the left and right sides
  • The polyphonic synth which plays the 3-note chords
  • Bass
  • A monophonic, airy sounding “ah” synth
  • A lead “sequencer” that plays in the center, with a 5th harmony that fades in and out
  • A short-tailed secondary lead layer
  • The warbly background synths on the left and right
• The 17 available chord progressions
• The overall structure of the piece
  • Fade-in
  • 5 parts
  • A “trigger” occurring at 3 specific points which activates one of the instrument mute sequences
  • A slowdown and fade-out for an ending

 

And here’s what the computer determines on each playthrough:

• Which chord progressions (of the 17 available) will be used for each of the 5 parts. There are no restrictions on which progressions can be used for each part, so:
  • The computer sometimes makes the piece have unique chord progressions for each part, creating a song structure of ABCDE
  • It is theoretically possible that the computer could choose the same chord progression for all 5 parts, creating AAAAA, though highly unlikely (odds of 1 in 1,419,817)
  • I am not well versed in the theory behind statistics, so I don’t know the reason for this, but the majority of the time, it tends to pick the same chord progression for at least two of the parts
    • Most often, it seems the structure will end up being something like ABCAD, or ABACB
• Unique melodies and rhythms for each instrument during each of the five parts of the song. That is:
  • A unique drum pattern for each individual drum sound during each part
  • A unique bass line during each part
  • A unique sequencer line for each part
  • A unique short-tailed synth line for each part
  • A unique set of warbly background notes on the left and the right for each part
• The morphing of the timbre of the instruments
  • What morphs:
    • The overtones that create the timbres
    • The amount and level of frequency and amplitude modulation
  • When this morphing occurs
• Where and when the instruments pan around in the stereo field
• When the sequencer harmony fades in and out
• Which instrument mute sequence (of the 3 available) occurs at each defined trigger point

 

FINAL NOTES / OTHER

 

There is one aspect of the composition that I listed under the “rules I chose” heading that I would actually consider some kind of middle ground: the available chord progressions. While I was working on coding the program, I made a chord progression generator. It automatically created bar-long chord progressions. Each time it would generate a loop, I would listen to it a few times and decide if I liked it or not. If I liked it, I would add it to the list of progressions that the computer could choose from. The ones that were musical nonsense were deleted. About 1/3 of the progressions generated by the algorithm I designed were usable. So in the end, I did choose the chord progressions that were included. But the computer created them in the first place.

On a different note, this method of presentation of the piece raises some art philosophy questions. Is the YouTube video of the piece being played actually the same piece? It’s not truly representative of the generative nature of the song; the YouTube video will be exactly the same every time it is played. It’s a facsimile that only demonstrates one particular runthrough. Eventually I’d like to make the jump over to Max/MSP, an extremely similar visual coding language that allows you to compile your code into a standalone program that anyone can run.

Lastly, all of the sounds you hear in the piece are generated via what is known as waveform synthesis. They are created by adding various combinations of sine waves and white noise‡ to one another. This creates complex waveforms which our ears interpret as different timbres. I could write a post entirely about how the sound generators in this piece work together to create the sounds that you hear, but this post is already long enough. Maybe for my next Pure Data based composition, I will focus my explanation entirely on that aspect of the piece.

 

‡ Sine waves are the most basic, pure waveform (a sinusoidal shape), and white noise is an audio signal that plays all frequencies at equal power (which ends up sounding like a sharp hiss). The audio demonstrations included in this article are all made up of basic sine waves.

 

 

 

Yikes! That’s a lot longer than I expected. Hopefully someone finds this interesting. At the very least, writing this cemented a bunch of this stuff in my brain.